Why the toothpick doesn't fall

Some days before, I had posted a demonstration of a tooth-pick contraption that is stable when it shouldn't be. Here is an image of the assembly, for recap.

A video of the demo is here :- https://lnkd.in/gUiNPKT

Blogging from the mobile app

We are accustomed to seeing things, supported like this fall - like the unfortunate person hanging on a cliff in the sketch below.

How does our demo survive? It must be something to do with the elaborate toothpick arrangement - but what is it exactly. There are 2 criteria for stability of a system, acted upon by forces, that obey Newton's Laws -

1) Force and Moment Equilibrium - ie The summation of forces along any arbitrary X, Y and Z axes, and that of moments should be zero. This is high-school physics. In the cliff-side sketch shown above - the unfortunate falling man will exert a non-zero "moment" about the fulcrum of the see-saw due to his own weight, and thus he will continue falling - unless his buddy reaches first and provides a counter moment.

2) Stable Equilibrium - A system is said to be in stable equilibrium if it satisfies 1 - and additionally, if perturbed from it's equilibrium position - restoring forces appear that push it back to the equilibrium position. See below sketch for 2 systems that are in equilibrium, but one is in stable equilibrium, while other isn't.

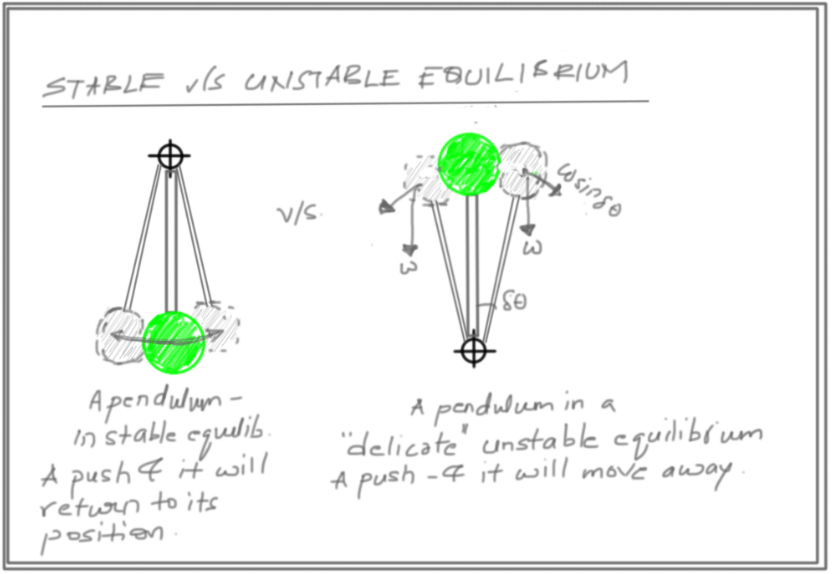
Not only is the toothpick system in equilibrium - it is in Stable equilibrium. That is why it does not fall even if nudged, or by gusts of wind. After having set this background, let us see why.

1) PROVING EQUILIBRIUM - SUMMATION OF FORCES AND MOMENTS ARE ZERO.

There are 3 forces in action here -

i) N = normal force exerted by the tabletop edge on the toothpick at the fulcrum

ii) f = friction force exerted by the table top edge on the toothpick at the fulcrum

iii) W = weight of the bottle + thread

The magic sauce is that the toothpick arrangement makes it possible for the thread to lie DEAD underneath the fulcrum point, thus W exerts no moment on the fulcrum. Hence, moment equilibrium(the difficult bit) is established about the fulcrum.

Please re-read the earlier sentence. And then see the diagrams below. Force equilibrium then is trivial.

FORCE EQUILIBRIUM IS THEREFORE ESTABLISHED.

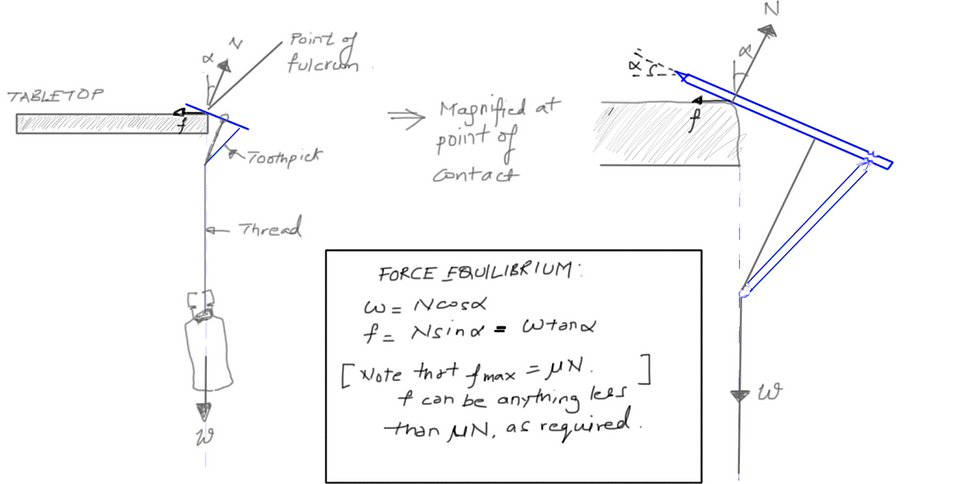
2) WHY IS THIS A STABLE EQUILIBRIUM?

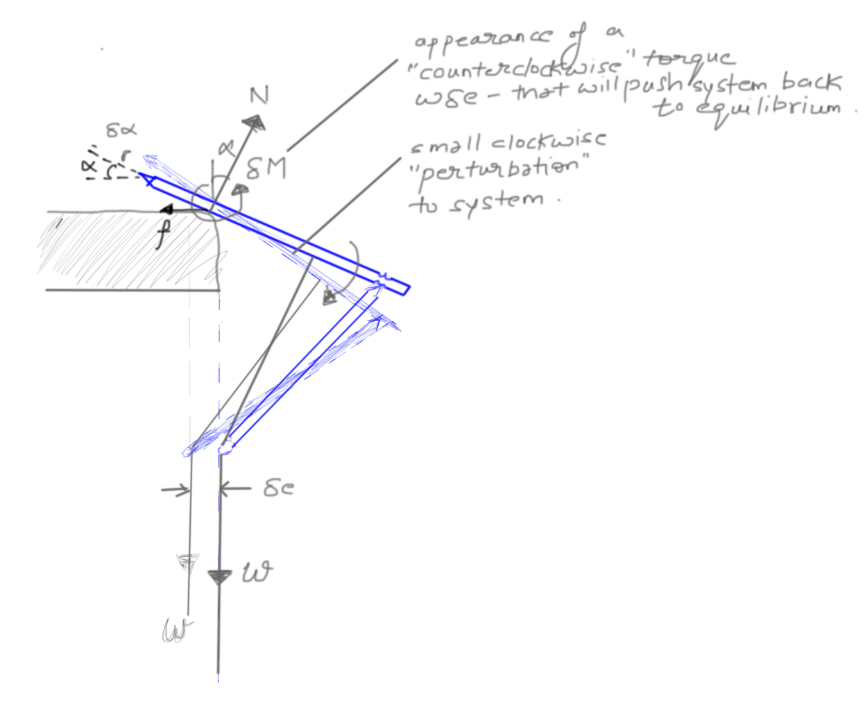
Lets think what happens if the system sways a little bit "clockwise" from it's equilibrium position ie, we perturb the equilibrium by a small amount.

As the toothpicks rotate clockwise, now the thread is no longer EXACTLY below the fulcrum point. It moves to one side and a torque appears about the fulcrum. But lo and behold, the torque is anti-clockwise - See the below sketch to understand why. This is related to the rigid-bent structure of the toothpicks. And, the anticlockwise torque - created on a clockwise rotational perturbance, pushes backs the system towards the equilibrium point.

And the toothpick doesn't fall.

Some more things worth thinking in this demonstration are :-

How does the system know to align itself the way it does? This has something to do with - the fact that - left to itself - a mechanical system auto-searches what is the minimum potential energy state for it to be in - if such a state exists, and it is kinematically possible for the system to attain it - it will attain it on it's own!